1. 数学定义
时间序列(Time Series)是一组按时间顺序排列的观测值集合,记为: $${X_t}, \quad t \in T$$ 其中,$T$ 为时间索引集(如分钟、日、年),$X_t$ 是时间点 $t$ 的随机变量。
2. 核心性质
时间序列分析的关键在于理解其统计特性,以下为四大核心性质:
平稳性(Stationarity)
- 严平稳:序列的联合分布不随时间平移改变
- 弱平稳(二阶平稳):满足以下两条件: $$E(X_t) = \mu \quad (\text{均值恒定})$$ $$Cov(X_t, X_{t+k}) = \gamma(k) \quad (\text{协方差仅与时滞k有关})$$
- 重要性:多数模型(如ARIMA)要求数据平稳
- 检验方法:ADF检验(Augmented Dickey-Fuller Test)
from statsmodels.tsa.stattools import adfuller result = adfuller(ts) print('ADF Statistic:', result[0]) print('p-value:', result[1]) # p<0.05则拒绝非平稳假设自相关性(Autocorrelation)
- 定义:时间序列与其自身滞后版本的相关性
- ACF(自相关函数):
$$\rho(k) = \frac{Cov(X_t, X_{t+k})}{\sqrt{Var(X_t)Var(X_{t+k})}}$$ - PACF(偏自相关函数):排除中间滞后影响后的相关性
- 作用:识别ARIMA模型的阶数(p, q)
季节性(Seasonality)
- 定义:固定周期内重复出现的模式(如月度、季度)
- 示例:零售销售额在每年12月达到峰值
- 检测方法:傅里叶变换、季节性子图(Seasonal Subseries Plot)
记忆效应(长期依赖)
- 定义:当前值与遥远过去值的相关性(如Hurst指数$H>0.5$)
- 量化方法:
$$H = \frac{\log(R/S)}{\log(T)} \quad (R: 极差, S: 标准差, T: 时间长度)$$
3. 时间序列分解
通过加法或乘法模型分解时间序列,识别趋势、季节性和随机成分(噪声、残差)。
加法模型(Additive Decomposition)
$$X_t = Trend_t + Seasonality_t + Residual_t$$- 适用场景:季节波动幅度不随时间变化
乘法模型(Multiplicative Decomposition)
$$X_t = Trend_t \times Seasonality_t \times Residual_t$$- 适用场景:季节波动幅度随趋势增长而扩大
STL分解(Seasonal-Trend decomposition using LOESS)
- 优势:可处理复杂季节性和非固定周期
- Python实现:
from statsmodels.tsa.seasonal import STL import matplotlib.pyplot as plt # 生成示例数据(包含趋势、季节性和噪声) np.random.seed(42) t = np.arange(100) trend = 0.1 * t seasonal = 5 * np.sin(2 * np.pi * t / 12) noise = np.random.normal(0, 1, 100) ts = trend + seasonal + noise # STL分解 stl = STL(ts, period=13) # 假设周期为13个时间单位 result = stl.fit() result.plot() plt.show() - 输出解析:
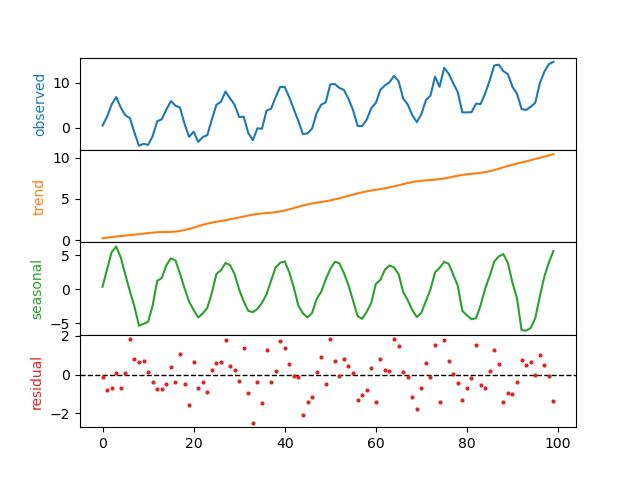
- 趋势(Trend):长期上升/下降模式
- 季节性(Seasonal):周期性波动
- 残差(Residual):去除趋势和季节后的随机波动
4. 时间序列预测模型
- 模型汇总表
| 模型 | 适用场景 | 优点 | 缺点 | 典型应用案例 |
|---|---|---|---|---|
| ARIMA | 平稳单变量序列 | 简单易解释,计算快 | 仅处理线性关系 | 商品价格短期预测 |
| SARIMA | 含季节性的平稳序列 | 直接建模季节性 | 参数选择复杂 | 月度电力需求预测 |
| VAR | 多变量动态系统 | 捕捉变量间相互作用 | 维度灾难,需平稳 | 宏观经济指标联合预测 |
| ETS | 趋势+季节明显的序列 | 计算高效,缺失数据鲁棒 | 无法加入外部变量 | 零售销售额预测 |
| Prophet | 含节假日效应的商业数据 | 直观调整节假日,自动化程度高 | 长期突变适应性差 | 节假日订单量预测 |
| LSTM | 复杂非线性序列 | 自动学习长期依赖,支持多特征 | 需大数据,黑箱模型 | 股价趋势预测 |
| Transformer | 超长序列全局依赖 | 并行计算,全局信息捕捉 | 资源消耗大,局部模式弱 | 多站点气象预测 |
| GARCH | 金融波动率建模 | 精确描述波动聚类 | 需结合均值模型 | 期权定价与风险管理 |
5. 时间序列分析在量化交易中的应用
量化交易依赖历史数据分析预测未来走势,时间序列分析在以下方面发挥关键作用:
- 价格预测:使用ARIMA、指数平滑预测股票价格,辅助买卖决策。
- 模式识别:识别均值回归、动量等交易模式。
- 波动率建模:GARCH模型预测波动率,管理风险。
- 策略开发:如配对交易,利用协整关系交易价差。
以下是几种最常见的策略及其时间序列模型支持:
均值回归策略
- 原理:资产价格偏离均值后会回归均值。
- 模型:AR(1)模型, $r_t = \phi r_{t-1} + a_t$,需 $ |\phi| < 1 $ 确保均值回归。
- 实现:计算时间序列均值。检查当前值是否偏离均值超过阈值。偏高卖出,偏低买入,预期回归。
- 半衰期: $h = -\ln(2)/\ln(\phi)$ ,决定持仓时间。
- 实例:股票价格高于一年均值,卖出预期回归。
动量策略
- 原理:近期表现好的资产继续表现好。
- 模型:移动平均线,短周期MA(如50天)与长周期MA(如200天)交叉。
- 实现:例如,计算50天和200天移动平均线(MA)。短MA上穿长MA(黄金交叉)买入,下穿(死亡交叉)卖出。
- 实例:50天MA上穿200天MA,买入股票预期继续上涨。
波动率交易
- 原理:从波动率变化中获利。
- 模型:GARCH(1,1),$ \sigma_t^2 = \omega + \alpha \epsilon_{t-1}^2 + \beta \sigma_{t-1}^2$
- 实现:预测高波动期买入期权,低波动期卖出。
- 实例:预测波动率上升,买入跨式期权(straddle)获利。
配对交易
- 原理:寻找协整的资产对,交易价差回归。
- 模型:协整检验(如Johansen检验),价差为平稳序列。
- 实现:价差高于均值+标准差k时卖出A买入B,低于均值-k标准差时反向。
- 实例:可口可乐和百事可乐价格协整,价差偏离时交易。