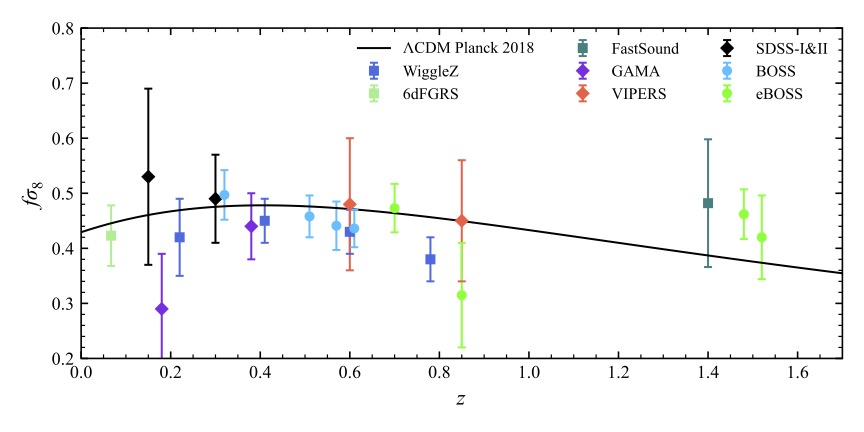
Both dark energy and modified gravity can interpret the cosmic acceleration, yet they predict the different growth histories of the structure. In observation, one can test the structure growth rate ($f\sigma_8$) through redshift-space distortion (RSD) effect to distinguish different cosmological models(Fig.1).

The observed position of the galaxy is distorted by its peculiar velocity along the line of sight.

\[\mathbf{s}=\mathbf{x}+\frac{\mathbf{v}_z}{aH}\]

Here, $\mathbf{x}$ is the real space position, $\mathbf{s}$ is the distorted position in redshift space, $\mathbf{v}_z$ is the peculiar velocity along the line of sight direction; $H$ is Hubble parameter, and $a$ is the scale factor.

RSD effect was first discovered in Jackson, J.C. 1972’s paper, a critique of rees’s theory of primordial gravitational radiation. The very sparse distributed galaxies already exhibit a directional arrangement along the line of sight, known as the Finger of God effect today.

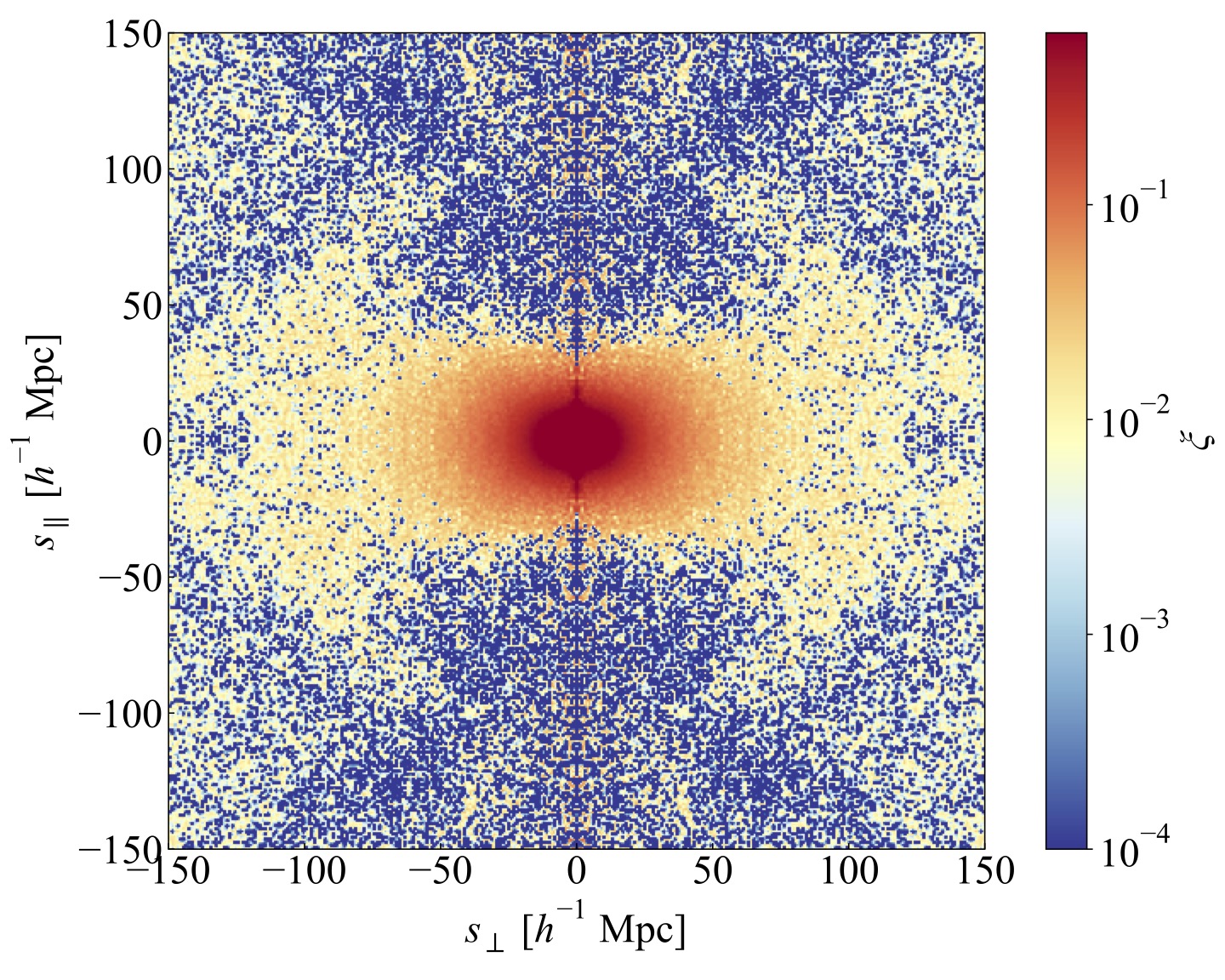
RSD effect modifies the galaxy clustering in redshift space, turns the isotropically distributed pattern of galaxies in real space into anisotropic in redshift space (Fig.2).

In statistics, correlation function and its Fourier transformation, power spectrum, can be used to describe the galaxy clustering. The definition of 2-point correlation function is

\[\xi(\mathbf{r})=\langle\delta(\mathbf{x})\delta(\mathbf{x+r})\rangle\]

Its Fourier counterpart, power spectrum $P(\mathbf{k})$ is defined by

\[\langle\delta(\mathbf{k})\delta(\mathbf{k}')\rangle=(2\pi)^3\delta_{3D}(\mathbf{k}+\mathbf{k}')P(\mathbf{k})\]

Fig.2 illustrates the 2D correlation function in redshift space.