3 宇宙学观测
目前人类对宇宙的探测手段主要有四种:
天体的电磁辐射。 目前,宇宙学观测仍主要依赖于天体的电磁辐射。 电磁辐射按照波段划分为不同类型,见表3.1。 受限于大气吸收的影响,地面望远镜主要针对可见光(光学,Optical)波段以及射电(Radio)波段进行观测。
引力波。 2015年,LIGO实验组观测到了第一个引力波事件(B. P. Abbott, Abbott, Abbott, Abernathy, et al., n.d.),从此打开了一个探测宇宙的新窗口。 引力波事件在宇宙中十分普遍,随着探测技术的进步,未来在宇宙学中的应用会更加重要;
宇宙线。 宇宙线是宇宙中的高能亚原子粒子,在宇宙学中的应用有限;
中微子。 由于中微子散射截面极小,因此中微子探测极为困难 [^6];
显然,§1.1中介绍的各种宇宙学参数都是不可直接观测的量,如何建立理论与可观测量之间的联系是观测宇宙学的重要任务。
| \(\gamma\) ray | X ray | UV (Ultraviolet) | Optical | IR (Infrared) | Radio |
|---|---|---|---|---|---|
| \(<0.1\rm{nm}\) | \(0.1\sim 10\rm{nm}\) | \(10\sim 400\rm{nm}\) | \(400\sim 700\rm{nm}\) | \(700\rm{nm} \sim 1\rm{mm}\) | \(>1\rm{mm}\) |
Electromagnetic radiation classes.
3.1 宇宙学距离,本动速度与红移
定义天体距离观测者的共动距离(comoving distance) \[\chi(a)\equiv \int^{t_0}_t \frac{\rm{d} t'}{a(t')}=\int_a^{a_0} \frac{\rm{d} a'}{a'^2H(a')}\ .\] 共动距离不随宇宙的膨胀发生改变。 共动距离并不是可观测量,实际的可观测量是光度距离与角直径距离。 我们把光度\(L\)已知的天体称为标准烛光,定义光度距离(luminosity distance)为 \[d_{\rm L}\equiv \left(\frac{L}{4\pi F}\right)^{1/2}= \left\{\begin{array}{lcl} \sinh(\sqrt{\Omega_k}H_0\chi)/(H_0\sqrt{\Omega_k})/a & , & \Omega_\kappa >0 \\ \chi/a & , & \Omega_\kappa =0 \\ \sin(\sqrt{-\Omega_k}H_0\chi)/(H_0\sqrt{-\Omega_k})/a & , & \Omega_\kappa <0 \end{array}\right.\ .\] 其中,\(F\)为测得的光通量。 对于展源,若其特征尺度为\(l\),还可以测量其角直径距离(angular diameter distance) \[d_{\rm A}\equiv \frac{l}{\theta} = \left\{\begin{array}{lcl} a \sinh(\sqrt{\Omega_k}H_0\chi)/(H_0\sqrt{\Omega_k}) & , & \Omega_\kappa >0 \\ a \chi & , & \Omega_\kappa =0 \\ a \sin(\sqrt{-\Omega_k}H_0\chi)/(H_0\sqrt{-\Omega_k}) & , & \Omega_\kappa <0 \end{array}\right.\ .\] 其中,\(\theta\)为\(l\)的张角,是一个小量。 光度距离及角直径距离与时空曲率\(\Omega_k\)有关。
定义红移\(z\)为 \[1+z\equiv \lambda_{\rm obs}/\lambda_0=a(t_0)/a(t)\ ,\] 其中,\(\lambda_{\rm obs}\)为观测到的光子波长,\(\lambda_0\)为静止参考系下,即天体辐射光子时,光子波长。
在引力作用下,星系会产生本动速度(peculiar velocity) \(v_{\rm pec}\)。 本动速度会产生额外的多普勒红移\(z_{\rm pec}=v_{\rm pec}/c\),使得实际测得的红移为 \[1+z_{\rm obs}=(1+z_{\rm pec})(1+z_{\rm cos})\ .\] 其中,\(z_{\rm cos}\)为宇宙学红移。
3.2 宇宙学探针
利用观测数据区分不同宇宙学模型,确定宇宙学参数,需要借助各种宇宙学探针。 本节将介绍若干常用的宇宙学探针。
3.2.1 宇宙微波背景辐射
复合时期(\(z\sim 1100\))光子退耦合变为自由光子,之后被我们观测到,产生CMB图像。 因此,借助CMB,我们可以了解早期宇宙的信息。
![Planck 2018 CMB Temperature Map. [@PlanckCollaboration2020c]](intro/Planck_2018_T_CMB.png)
Figure 3.1: Planck 2018 CMB Temperature Map. (Planck Collaboration, Aghanim, et al., n.d.)
Alpher et al. (n.d.) 首先在理论上预言了宇宙微波背景辐射(CMB)的存在。 直到1965年,Penzias与Wilson在一次观测中意外发现了CMB(Dicke et al., n.d.; Penzias & Wilson, n.d.)。 目前最精确的CMB观测来自普朗克(Planck)卫星。 图3.1展示了普朗克2018年最新的观测结果(Planck Collaboration, Aghanim, et al., n.d.)。 CMB的平均温度\(T\sim 2.725\rm{K}\),温度涨落仅为\(\sim 10^{-5}\),这证明宇宙在大尺度上各向同性。 而小尺度上的各向异性主要来自于原初密度扰动,正是原初扰动促使结构在晚期形成。 统计上刻画小尺度上的各向异性可以利用CMB图像的角功率谱。 将温度涨落展开为球谐函数 \[\frac{\Delta T}{T}=\sum_{\ell=1}^\infty \sum_{m=-\ell}^{\ell} a_{\ell m}Y_{\ell m}(\theta, \psi)\ ,\] 其中,\(\ell\)与\(m\)为整数,\(a_{\ell m}\)为展开系数,\(\theta\)与\(\psi\)为方位角。 角功率谱的定义为 \[C_{\ell} = \frac{1}{2\ell +1}\sum_m |a_{2m}|^2\ .\]
![Planck 2018 CMB temperature angular power spectrum [@PlanckCollaboration2020b]. Data points are measured from the Planck observation. The blue curve is the best-fit LCDM theoretical spectrum. The lower panel is the residual error.](intro/coadded_TT.png)
Figure 3.2: Planck 2018 CMB temperature angular power spectrum (Planck Collaboration, Akrami, et al., n.d.). Data points are measured from the Planck observation. The blue curve is the best-fit LCDM theoretical spectrum. The lower panel is the residual error.
CMB角功率谱的形状主要由以下几个效应决定: (1)功率谱中的振荡来自于下文 (§1.2.2.2) 将要介绍的重子声波振荡(Baryon Acoustic Oscillation,BAO); (2)描述光子受最后散射面上引力势影响的SW效应; (3)光子在最后散射面上的多普勒效应; (4)随着光子退耦,光子自由程逐渐增大,导致小尺度上的扰动被抹平的Silk Damping; (5)描述光子在传播路径上受引力势影响的ISW效应(Dupé et al., n.d.; Sachs & Wolfe, n.d.); (6)CMB光子与再电离后的电子发生逆康普顿散射产生的SZ效应(Carlstrom et al., n.d.)等。 其中,(5,6)为二阶(secondary anisotropies)效应。 图3.2展示了Planck 2018 测得的CMB角功率谱。 当\(\ell<30\)时误差棒显著增大,这是由于实际观测中,我们只能观测到一个宇宙所引起的cosmic variance。 图中的实线为\(\Lambda\)CDM模型的最佳拟合结果。 表3.2列出了Planck 2018在\(\Lambda\)CDM模型假设下得到的6个独立宇宙学参数, 分别为重子密度\(\Omega_{\rm b}h^2\),暗物质密度\(\Omega_{\rm c}h^2\), 复合时期声视界(参见§1.2.2.2)张角\(100\theta_{\rm MC}\), 再电离光深\(\tau\),原初扰动振幅\(A_s\),以及标量谱指数\(n_s\)[^7]。
| \[\Omega_b h^2\] | \[\Omega_c h^2\] | \(100\theta_{\rm{MC}}\) | \(\tau\) | \(\ln(10^{10}A_s)\) | \[n_s\] |
|---|---|---|---|---|---|
| \(0.02233\) | \(0.1198\) | \(1.04089\) | \(0.0540\) | \(3.043\) | \(0.9652\) |
| \(\pm 0.00015\) | \(\pm 0.0012\) | \(\pm 0.00031\) | \(\pm 0.0074\) | \(\pm 0.014\) | \(\pm 0.0042\) |
3.2.2 重子声波振荡
复合发生以前,物质与光子处于高温高压的耦合态。 在原初扰动作用下,高密度区域物质趋于聚合。 当聚合到一定程度时,由于光压的作用,重子物质开始向外扩散。 随着扩散光压减弱,在引力作用下重子再次趋于聚合,如此反复,产生了一个由高密度区域向外传播的振荡波。 类比于声波,我们将这种效应称之为重子声波振荡(Baryon Acoustic Oscillation,BAO)。 振荡传播的速度称为声速\(c_s\),由重子与光子的能量密度比\(\rho_{\rm b}/\rho_{\gamma}\)决定: \[c_s(z)=\frac{c}{\sqrt{3}}\left(1+\frac{3\rho_{\rm b}}{4 \rho_{\gamma}}\right)^{-\frac{1}{2}}\ .\]
复合发生后,光子退耦合。 由于损失了光压,重子扰动被固定在了一个以初始扰动位置为中心的球壳上。 球壳的半径为此时声波传播的距离,称为声视界: \[r_s=\int^{t_*}_0 \frac{c_s(t)}{a(t)}\rm{d} t = \int^\infty_{z_*}\frac{c_s(z)}{H(z)}\rm{d} z\] 其中,下标\(_*\)代表该量为复合时期的量。 声视界在共动坐标下保持不变,目前测得的值约为\(r_s \approx 147\)Mpc (Planck Collaboration, Akrami, et al., n.d.)。
1960年代晚期,在CMB中最早预言了重子声波振荡的存在。 2000年,(de Bernardis et al., n.d.)利用回力镖气球实验(BOOMERanG),第一次在CMB功率谱中探测到了BAO峰。 光子退耦后,重子声波振荡的遗迹会保留至今,因此BAO也会体现在大尺度结构中。
描述大尺度结构常用的两个统计量是关联函数和功率谱。 定义星系的密度扰动场 \[\delta_g=\frac{n_g-\bar{n}_g}{\bar{n}_g}\ .\] 其中,\(n_g\)为星系数密度。星系的两点关联函数定义为 \[\xi_g({\bf r})=\langle \delta_g({\bf x})\delta_g({\bf x}+{\bf r})\rangle_{{\bf r}}\ .\] 其中,\(\langle\cdots\rangle_{\bf r}\)表示对所有间隔为\({\bf r}\)的星系对求平均。 两点关联函数反映了在空间中任意间隔为\({\bf r}\)的两点上找到一对星系的概率与假设星系随机分布时在同样间隔找到一对星系的概率之差。 因此,关联函数直接反映了星系在位形空间中的成团性。 星系功率谱\(P_g({\bf k})\)的定义为 \[\langle \delta_g({\bf k})\delta_g({\bf k}')\rangle=(2\pi)^3 \delta_{\rm 3D}({\bf k}+{\bf k}')P_g({\bf k}) \ .\] 功率谱与关联函数可以通过傅立叶变换相互转换。功率谱也反映了星系在不同尺度上的成团性。 如果宇宙学原理成立,那么关联函数与功率谱也应当各向同性, 但是,由于星系本动速度的影响,实际观测中存在导致各向异性的红移畸变效应(参见§1.2.2.3)。
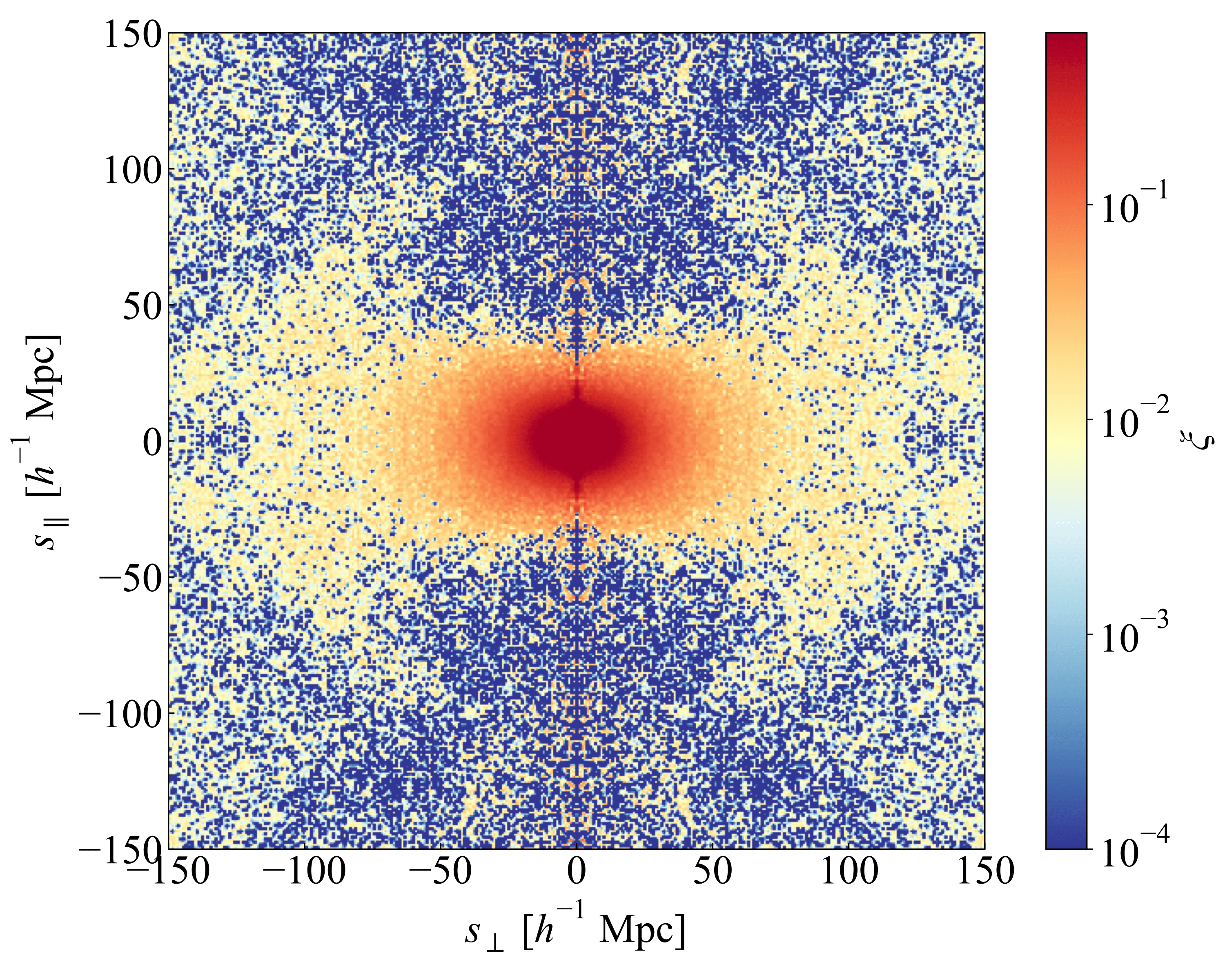
Figure 3.3: 2 dimensinal 2-point correlation function in redshift space for BOSS CMASS Galaxies.
图3.3为我们利用观测数据计算得到的星系二维关联函数,横纵坐标分别对应垂直视线方向及平行视线方向,\(s\)表示红移空间中的坐标。 可以明显的看到,在\(\sim 100 \rm{Mpc}/h\),由于BAO的影响,关联函数增强; 同时,由于红移畸变的影响,关联函数并非各向同性,而是沿视线方向产生了畸变。
![Monople (blue), quadrupole (red) and hexadecapole (grey) of correlation function (left) and power spectrum (right) measured for eBOSS quasar samples [@Hou2021; @Neveux2020]](intro/dr16_qso_pk3m.png)
Figure 3.4: Monople (blue), quadrupole (red) and hexadecapole (grey) of correlation function (left) and power spectrum (right) measured for eBOSS quasar samples (Hou et al., n.d.; Neveux et al., n.d.)
实际应用中,通常不会使用\((s_{\bot}, s_{\|})\)的投影方式,而是计算\(\xi(s, \mu)\),其中,\(\mu\)为\({\bf s}\)与视线方向夹角的余弦。 直接拟合\(\xi(s, \mu)\)比较困难,因此还会利用勒让德多项式的正交性,进一步计算关联函数的多极距(multipoles) \[\xi_\ell(s)\equiv \frac{2\ell+1}{2}\int_{-1}^1 \xi(\mu, s)\mathscr{P}_\ell (\mu)\rm{d} \mu \ ,\] 其中,\(\mathscr{P}_\ell\)为\(\ell\)阶勒让德多项式。 由于对称性,关联函数只存在偶极矩\(\ell=0, 2, 4\dots\)。 同理,也可以计算功率谱的多极距\(P_{\ell}(k)\)。 图3.4为利用eBOSS Quasar观测数据测得的关联函数及功率谱的多极距。 由于暗物质背景的作用,相比CMB,BAO的信号在大尺度结构中被严重削弱。 在功率谱中,BAO造成的扰动约为\(\sim 10\%\)。 在关联函数中,\(s\sim 100\rm{Mpc}/h\)处对应的峰为BAO峰。
![Angular diameter distance and Hubble distance measured with BAO from different samples at different redshifts [@Hou2021]. The curves are the predictions of Planck 2018 LCDM model.](intro/bao_distance_ebossdr16_pllik18.png)
Figure 3.5: Angular diameter distance and Hubble distance measured with BAO from different samples at different redshifts (Hou et al., n.d.). The curves are the predictions of Planck 2018 LCDM model.
在计算距离时,需要设定基准(fiducial)宇宙学,这会同时给定基准声视界的大小。 定义参数\(\alpha\)为测定的BAO尺度与基准宇宙学给出的尺度之比。 对于各向异性的关联函数,分别定义垂直/平行视线方向的两个参数 \[\alpha_{\bot}=\frac{D_M(z)/r_s}{D_M^{\rm fid}(z)/r_s^{\rm fid}}\ ,\quad \alpha_{\|}=\frac{D_H(z)/r_s}{D_H^{\rm fid}(z)/r_s^{\rm fid}}\ .\] 其中,\(D_M\)为共动角直径距离,\(D_H=c/H\) 为哈勃距离,上标\(\rm fid\)代表基准宇宙学。 \(\alpha_{\|}, \alpha_{\bot}\)被称为AP参数(Alcock & Paczynski, n.d.)。 在限制宇宙学时,需要将所有由基准宇宙学计算得到的距离转换为带AP参数的距离, 如\(\xi(s_\bot, s_{\|})\to \xi(\alpha_{\bot} s_\bot, \alpha_{\|}s_{\|})\)。 BAO被称为”标准尺”,通过测量哈勃距离\(D_H\)及角直径距离\(D_M\)来限制宇宙学。 图3.5展示了不同观测数据中,BAO对哈勃距离\(D_H\)及角直径距离\(D_M\)的测量。 其中,实线为Planck 2018 \(\Lambda\)CDM模型参数的预测结果。
3.2.3 红移畸变
![Illustration of redshift space distortion [@Hamilton1998]. The curves are the predictions of Planck 2018 LCDM model.](intro/rsd_interp.png)
Figure 3.6: Illustration of redshift space distortion (Hamilton, n.d.). The curves are the predictions of Planck 2018 LCDM model.
如§1.2.1所述,本动速度会在宇宙学红移上叠加额外的多普勒红移, 因此在实际观测中,星系的观测位置会由于本动速度的作用而偏离其真实位置。 红移空间中的位置\({\bf s}\) 与真实空间中的位置\({\bf x}\)存在以下关系: \[{\bf s}= {\bf x}+ \frac{v_{\|}}{aH(z)}\hat{x}\ .\] 其中,\(v_{\|}\)为本动速度沿视线方向\(\hat{x}\)的投影。 这带来的直接影响是改变了星系各向同性的空间分布,这种效应被称为红移畸变。
图3.6为产生红移畸变的示意图。其中,视线方向由下而上,蓝色箭头代表本动速度的方向。 图中自上而下对应的尺度依次减小。 在线性尺度,星系有向高密度区域聚合的趋势,因此在红移空间中,星系分布在视线方向上被压缩,导致测得的成团性加强,这种效应被称为Kaiser效应。 随着尺度的减小,星系的随机运动逐渐增强,这使得达到一定非线性尺度时,星系原有的成团性在红移空间中会被打破。 这种效应使星系分布在视线方向被拉长,像手指一样指向观测者,所以被称为Finger-of-God效应。 在二维关联函数中(图 3.3),可以看到Kaiser及FoG对星系分布造成的影响。
| Cosmological Probes | Measurements | Main Systematics | |
|---|---|---|---|
| CMB | Primodial | \(T,P\) | Foreground, equipment Calibration |
| ISW | \(T\to \dot{\phi}\) | Cosmic variance | |
| tSZ | \(T\to P_{\rm gas}\), | Foreground, baryon physics | |
| kSZ | \(T\to P_{\hat{v}_e}\), | Foreground, baryon physics | |
| lensing | \(T,P \to \kappa\) | Foreground, baryon physics | |
| Lensing | weak | \(\gamma,\kappa \to d_{\rm A}, D\) | Shape, photometry, baryon physics, IA |
| strong | \(\Delta t \to H\) Sh | ape, photometry, baryon physics | |
| Galaxy Clutering | smooth | \(P_g\to d_{\rm A} H\) | NLinear NLocal bias |
| BAO | \(P_g\to d_{\rm A},H\) | NLinear evolution, NLinear NLocal bias | |
| RSD | \(P_g\to P_v\) | NLinear evolution, NLinear NLocal bias | |
| Ia SN | \(m, z \to d_{\rm L}\) | Standard candle, photometry | |
| Galaxy Cluster | \(n(z)\) | Mass Calibration | |
| Gravitational Waves | Primordial | CMB B-mode \(\to r\) | Sensitivity, foreground, instrument systematics |
| Local | \(h(t)\to d_L\) | Sensitivity, foreground, instrument systematics |
上文主要介绍了三个宇宙学探针。 宇宙微波背景辐射与宇宙大尺度结构形成关系密切,给出了宇宙演化的初始条件; 而重子声波震荡与红移畸变则直接描述了大尺度结构中的星系成团性。 其中,红移畸变在结构增长的研究中十分关键,也是本文研究的重点,会在第二章中详细介绍。