2 宇宙学模型
上世纪80年代以来的宇宙学观测表明了我们所处的宇宙正在加速膨胀 (Hinshaw et al., n.d.; Ivanov et al., n.d.; Perlmutter et al., n.d.; Planck Collaboration, Aghanim, et al., n.d.; Riess et al., n.d.; Spergel et al., n.d.),如何解释宇宙加速膨胀成为了现代天文学中的重要课题, 其中,最有力的手段之一就是对宇宙大尺度结构的观测及研究。 本章将简要介绍标准宇宙学模型、以及若干替代模型。
2.1 标准宇宙学模型
宇宙学基本原理指出:宇宙在大尺度上均匀且各向同性[^1]。 满足宇宙学基本原理的度规为弗里德曼-勒梅特-罗伯逊-沃尔克(Friedmann–Lemaître–Robertson–Walker, FLRW)度规[^2]: \[\label{eqn:flrw} \rm{d} s^2 = -\rm{d} t^2 + a^2(t)\left[\frac{\rm{d} r^2}{1-\kappa r^2}+r^2\rm{d} \theta^2 +r^2\sin^2\theta \rm{d} \phi^2 \right]\ ,\] 其中,\(a(t)\)为尺度因子。规定\(a_0\equiv a(t_0)=1\),\(t_0\)为现在时刻。 \(\kappa\)为时空曲率,\(\kappa<0\)为开放宇宙,\(\kappa=0\)为平直开放宇宙,\(\kappa>0\)为闭合宇宙。
求解爱因斯坦场方程 \[\begin{align} G_{\mu\nu}\equiv R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R = -8\pi G T_{\mu\nu} \ , \tag{2.1} \end{align}\] 可以得到弗里德曼方程组 \[\begin{align} H^2 + \frac{\kappa}{a^2} &= \frac{8\pi G}{3} \sum_i \rho_i \label{eqn:friedmann} \ ,\\ \frac{\ddot{a}}{a} &= -\frac{4\pi G}{3}\sum_i(\rho_i+3p_i) \label{eqn:friedmann_acc} \ . \tag{2.2} \end{align} \] 其中,\(H\equiv\dot{a}/a\)为哈勃参数,描述宇宙的膨胀速率。 \(T_{\nu}^{\mu}={\rm diag}(-\rho,p,p,p)\)为能量动量张量。 \(\rho=\sum_i\rho_i\),\(p=\sum_i p_i\), \(\rho_i\)与\(p_i\)分别为宇宙中不同组分的能量密度与压力。 定义临界密度 \[\rho_c(a)\equiv \frac{3H^2}{8\pi G}\ ,\] 那么每个组分的无量纲能量密度可以写为\(\Omega_i(a)\equiv \rho_i/\rho_c\)。 设总能量密度\(\Omega(a)\equiv \sum_i\Omega_i(a)\),则根据弗里德曼方程的限制, \[1=\sum_i \Omega_i(a)+\Omega_{\kappa}(a)\equiv \Omega(a)+\Omega_{\kappa}(a)\ .\] 其中,\(\Omega_{\kappa}(a)\equiv -\kappa /(a^2 H^2)\)。 各组分的演化由初始条件及对应的状态方程\(w_i\equiv p_i/\rho_i\)决定。 初始条件一般设置为现在时刻。 称\(H_0\equiv H(a=1)\)为哈勃常数,通常使用其参数化形式\(H_0=100h {\rm (km/s/Mpc)}\),\(h\)为无量纲哈勃参数。 另外,通常还把\(a=1\)时的各组分无量纲能量密度\(\Omega_i(a=1)\)简记为\(\Omega_i\)。
由能动张量守恒可得 \[\rho(a)=\rho(a_0)\exp\left[\int_{a}^{a_0}3(1+w(a))\frac{\rm{d} a}{a}\right]\ .\] 对于非相对论性粒子,\(w=0\),\(\rho \propto a^{-3}\); 对于光子和其他相对论性粒子,\(w=1/3\),\(\rho \propto a^{-4}\); 对于时空曲率\(\kappa\),\(w=-1/3\),\(\rho\propto a^{-2}\);
2.1.1 宇宙的加速膨胀
公式(2.2)描述宇宙膨胀的加速度,可根据状态方程进一步写为 \[\frac{\ddot{a}}{a} = -\frac{4\pi G}{3}\sum_i \rho_i(1+3 w_i)\ .\] 由于时空曲率项的状态方程\(w=-1/3\),因此曲率对加速度没有影响。 对于物质,\(\rho+3p\simeq \rho>0\),因此物质产生的加速度\(<0\),导致减速。 而多种宇宙学观测表明,宇宙正在加速膨胀 (Hinshaw et al., n.d.; Ivanov et al., n.d.; Perlmutter et al., n.d.; Planck Collaboration, Aghanim, et al., n.d.; Riess et al., n.d.; Spergel et al., n.d.), 因此宇宙中必然存在\(\rho+3p<0\)(即\(w<-1/3\))的成分,我们将这部分成分叫做暗能量。
目前最通行的暗能量候选体是宇宙学常数\(\Lambda\),其能量密度为\(\rho_{\Lambda}=-3\Lambda/(8\pi G)\)。 由于\(\Lambda\)不随时间变化,因此其状态方程\(w_{\Lambda}=-1\),即\(\Lambda\propto a^0={\rm const.}\)。 宇宙学常数并非唯一选项,可能的替代理论还有标量场理论quintessence(\(w> -1\)),幻影理论phantom(\(w<-1\)), quintom理论(\(w\)可以跨过\(-1\))等(参见§1.1.2)。
对于一个包含物质、辐射、曲率及宇宙学常数项的宇宙,弗里德曼方程可以重新整理为 \[\frac{H^2(a)}{H_0^2}=\Omega_{\rm m} a^{-3}+\Omega_{\rm R} a^{-4} +\Omega_{\kappa}a^{-2}+\Omega_{\Lambda}\ .\] 这里的\(\Omega_i\)均为\(a=1\)时的无量纲常数。 宇宙微波背景辐射(Cosmic Microwave Background, CMB)等观测 (Hinshaw et al., n.d.; Planck Collaboration, Ade, et al., n.d.; Planck Collaboration, Aghanim, et al., n.d.) 显示: (1) \(\Omega_{\rm m}\simeq 0.32\)。 物质中大部分是不能用标准粒子模型描述的冷暗物质(CDM)。 这些物质不发生电磁相互作用,因此不辐射/吸收光子, 又由于其运动速度远低于光速,因此温度较低,固被称作冷暗物质。 物质中的标准模型粒子今天在宇宙中的占比约为\(\Omega_b\simeq 0.05\)。 (2) \(\Omega_{\Lambda}\simeq 0.68\)。 宇宙学常数在今天为主导成分,是晚期宇宙的加速膨胀驱动力。 但宇宙学常数并非唯一选择,诸如修改引力等理论也可以提供晚期宇宙加速膨胀的机制。 (3) \(\Omega_{\kappa}\simeq 0\),即我们的宇宙是平直的。 (4) \(\Omega_R\simeq 10^{-4}\)。辐射曾经是宇宙的主导成分,但随着宇宙膨胀逐渐衰减,现在几乎可以被忽略。 上述主要由\(\Lambda\)与CDM主导的宇宙通常被称为标准宇宙学模型,记为\(\Lambda\)CDM模型。
2.1.2 宇宙的演化历史
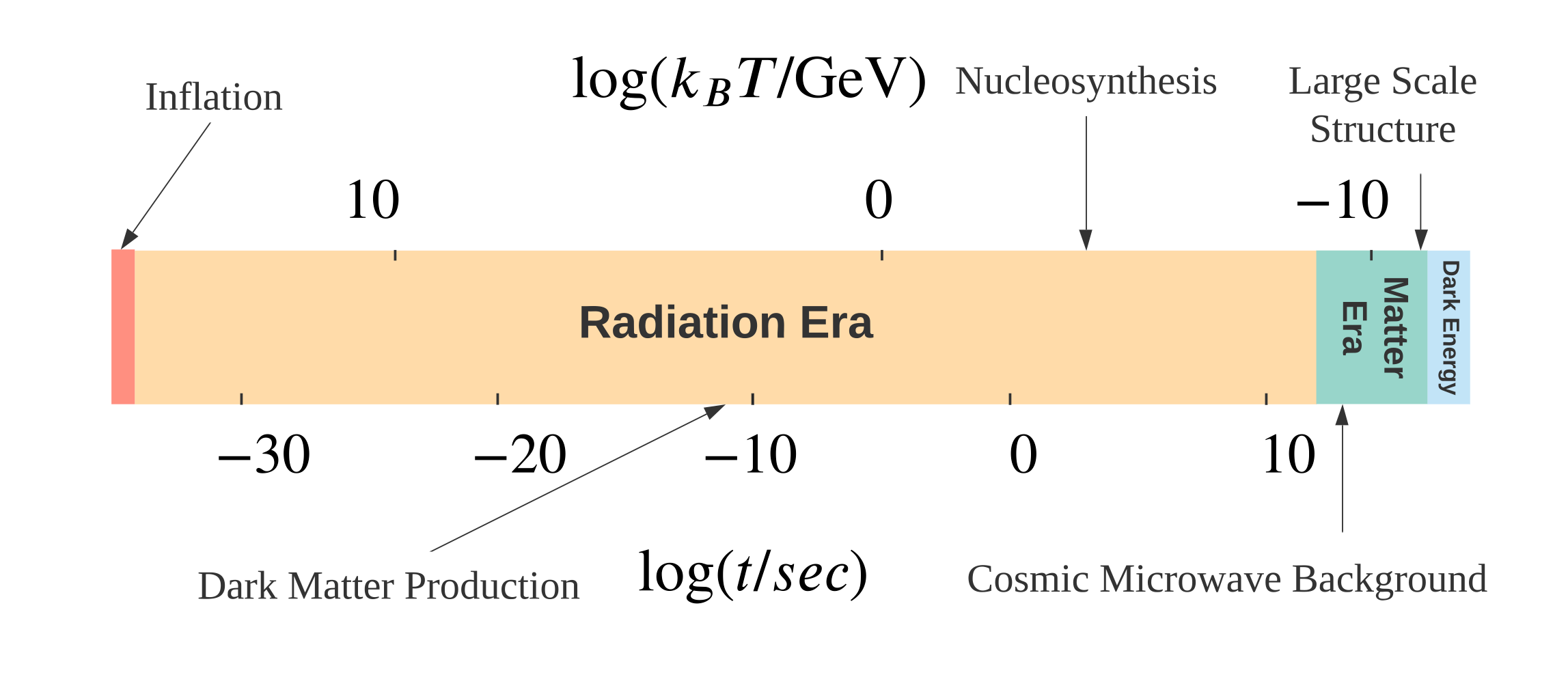
Figure 2.1: A histroy of the Universe. Any epoch can be associated with either temperature or time.
图2.1展示了目前广泛认可的宇宙演化历史。 现代宇宙学认为宇宙诞生于约138亿年前的一场大爆炸(Big Bang)。 大爆炸发生后,引力率先解耦,与大统一理论(Grand Unification Theory, GUT) (Patrignani et al., n.d.) 共同决定宇宙极早期的演化。 在\(10^{-35} \rm{s}\),温度下降到\(10^{27}\rm{K}\)时,宇宙进入暴涨[^3] 时期(Inflation) (Guth, n.d.; Linde, n.d.)。 这个阶段宇宙的体积在\(10^{-36}\sim 10^{-34}\rm{s}\)内极速膨胀了\(e^{\sim 65}\)倍,GUT解耦成为强相互作用与弱电相互作用
暴涨结束后,在\(10^{-33} \rm{s}\),宇宙进入辐射主导时期,暗物质可能产生于这一时期 (Bernal et al., n.d.; Hall et al., n.d.; Marsh, n.d.; McDonald, n.d.; Tenkanen, n.d.)。 当温度下降至\(10^{15} \rm{K}\approx 100{\rm GeV}\)时,电磁相互作用与弱相互作用解耦合,当今宇宙中的四种基本相互作用全部产生。 随后温度继续下降。在\(10^{-6}\rm{s}\),温度约\(10^{13}\rm{K}\)时,夸克冻结形成强子。 在\(10^{-2}\rm{s}\),温度约\(10^{11}\rm{K}\)时,质子与中子退耦合变为自由粒子。 在约\(1\rm{s}\)时,温度下降至\(10^{10}\rm{K}\),中微子从物质与辐射中退耦合[^4]。 同时自由中子变得不再稳定,衰变成为质子,电子与中微子,数量减小到质子的\(1/5\)。 在约\(3\)分钟时,温度下降至\(5\times 10^9 \rm{K}\),轻元素核合成(Nucleosynthesis)开始。 这一过程主要产生了\(^1\)H (约\(75\%\))与\(^4\)He (约\(25\%\)),以及极少量的\(^2\)H,\(^3\)He,\(^7\)Li与\(^7\)Be等元素[^5]。 这一时期的所有粒子都处于高温高密的等离子态,光子被束缚在等离子流体内,无法自由传播。
进入物质主导的时期后,当宇宙温度进一步下降至\(\sim 3000\rm{K}\)时,自由电子与原子核结合形成电中性原子。 辐射从物质中退耦合,自由光子产生。这是我们可以观测到的最早的电磁信号。 此时是大爆炸发生后的约38万年,这一时期被称为复合(Recombination)时期, 自由光子在产生时所处的时空曲面被称为最后散射面(Last Scattering Surface,LSS)。 从复合时期到第一代恒星形成,H与He均以电中性形态存在。除中性氢的\(21\rm{cm}\)辐射外 (Scott & Rees, n.d.; Subramanian & Padmanabhan, n.d.), 宇宙中几乎没有新的可见光或红外辐射产生。这一时期被称为宇宙的黑暗时期(Dark Age)。 在大爆炸发生后的约4-5亿年,宇宙温度下降至\(\sim 30\rm{K}\), 原初扰动在引力作用下逐渐形成结构,并在其中孕育出了第一代星系与恒星,宇宙再次被点亮。 伴随着超新星的爆发,金属元素产生,行星、恒星、星系等结构大量形成。 期间,恒星形成时产生的高能光子导致中性氢再次被电离,产生自由电子与氢原子核, 这一时期被称为再电离时期(Epoch of Reionization,EoR) (D. H. Weinberg et al., n.d.)。 最后散射面发出的光子与这些自由电子发生逆康普顿散射, 并在今天看到的宇宙微波背景辐射中留下痕迹。
现在的宇宙距大爆炸约138亿年,正处于低物质密度、低辐射密度(温度约为\(2.725\rm{K}\)),由暗能量主导的时期。 在暗能量的作用下,宇宙将继续加速膨胀。
2.1.3 标准宇宙学存在的问题
标准宇宙学模型在解释上述各阶段的宇宙学观测数据时取得了巨大成功,但也存在许多问题,其中最直接的一个就是宇宙学常数问题 (S. Weinberg, n.d.)。 观测上利用\(\Lambda\)CDM模型得到的暗能量密度为\(\rho_{\Lambda}^{\rm obs}\sim 10^{-47} \rm{GeV^4}\), 而基于粒子物理理论计算得到的期望值为\(\rho_{\Lambda}^{\rm exp}\sim 10^{72} \rm{GeV^4}\), 前者比后者小了\(\sim 120\)个数量级,二者巨大的差异难以调和。 与宇宙学常数问题相关的另一个问题是巧合问题 (Zlatev et al., n.d.)。 如前所述,物质的能量密度\(\rho_{\rm m}\)随着宇宙的膨胀不断下降。 在经历了138亿年的演化后,今天观测到的\(\rho_{\Lambda}\)与\(\rho_{\rm m}\)大小相当。 这意味着二者的比例在138亿年前的早期宇宙中必须是一个极小的特定值,增大或减小该数值都将改变宇宙的演化历史。 这一巧合令人难以理解。 为了解决这些问题,一方面需要尽量降低观测结果的系统误差,另一方面,人们也在寻求标准宇宙学模型之外的替代理论。
2.2 非标准宇宙学模型
2.2.1 标准宇宙学的简单唯象推广
在\(\Lambda\)CDM模型描述的宇宙中,暗能量状态方程为定值\(w=-1\), 这带来的一个直接问题就是上文中提到的宇宙学常数问题。 一个对\(\Lambda\)CDM模型的简单推广是将\(w\)看作任意常数,称为\(w\)CDM模型。 \(w\)也可以随时间演化,例如取\(w=w_0+w_a(1-a)\),称为\(w_0w_a\)CDM模型, 其中,\(w_0\)为\(t_0\)时的暗能量状态方程,\(w_a=-\partial w/\partial a\),\(a\)为尺度因子。 广义上\(w\)可以取任何形式。
2.2.2 其他模型
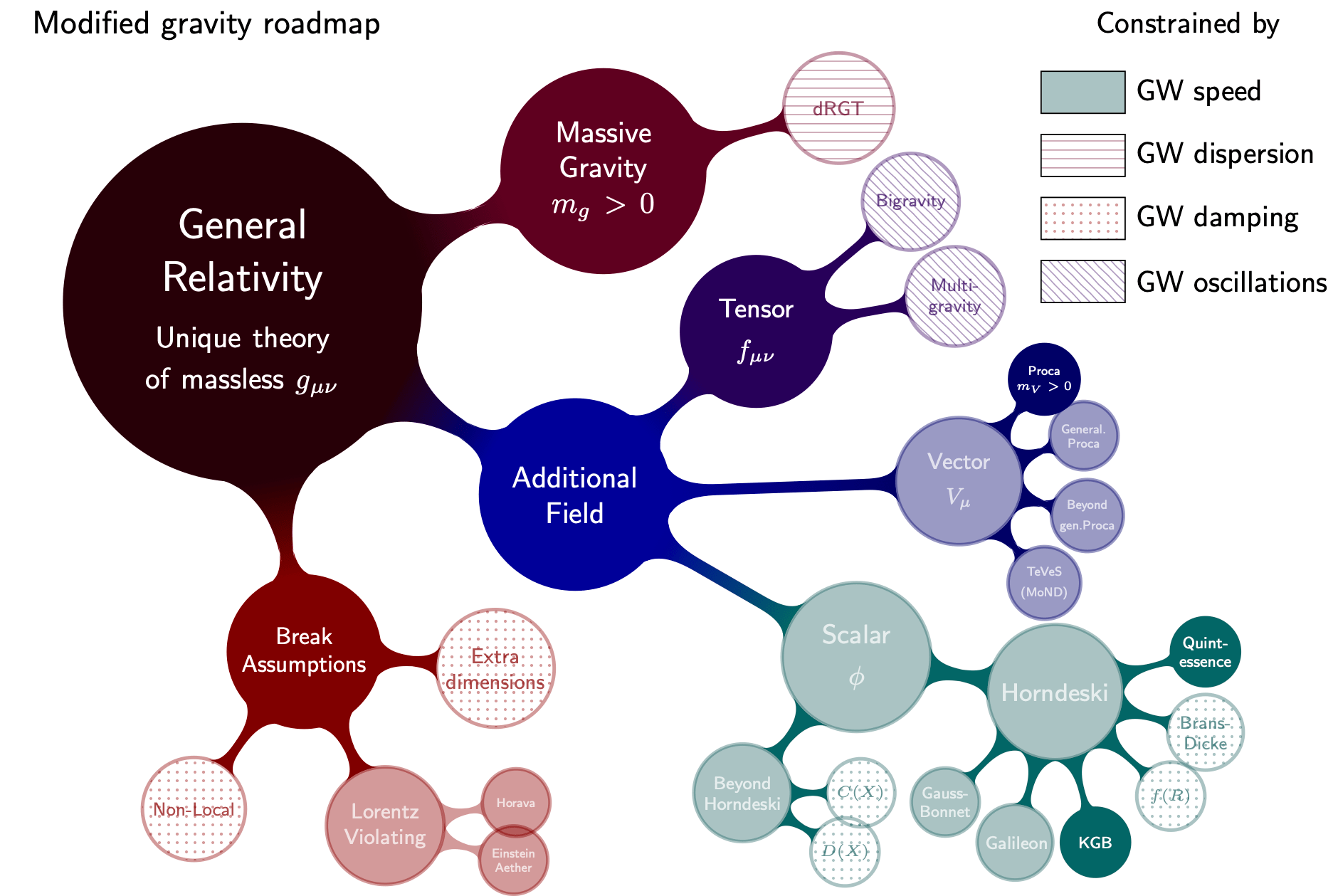
Figure 2.2: Modified Graivity Theories.
爱因斯坦场方程(公式(2.1))决定了宇宙演化的动力学。 通过修改场方程左右两侧\(G_{\mu\nu}\)及\(T_{\mu\nu}\),可以得到不同的宇宙学模型。 通过修改等式左侧\(G_{\mu\nu}\),可以得到一系列修改引力模型。 而在等式右侧\(T_{\mu\nu}\)中加入提供负压的成分,可以得到一系列暗能量模型。 例如标准宇宙学模型为了得到加速膨胀的宇宙学解,在\(T_{\mu\nu}\)中加入了宇宙学常数项\(\Lambda\)。
图2.2展示了修改引力的分支结构。 对广义相对论的修改通常有三大类:
打破原有广义相对论假设。如引入更高维度,DGP模型、弦论可以归结为这类。
引入附加场。附加场可以是标量场,如\(f(R)\)、\(f(\tau)\)` (Cai, Capozziello, et al., n.d.);也可以是矢量场,如 TeVeS/MOND;亦或是张量场。
引入带质量的引力子。如dRGT模型。
除此之外,还可以构建各种耦合模型,如曲率与物质场耦合模型\(f(R, T)\) (Amendola & Tsujikawa, n.d.-a; Harko et al., n.d.)。 也有建立在宇宙学基本原理之外的模型,如LTB模型,认为宇宙各向同性但径向非均匀。 另外,利用有效场理论(Effective Field Theory,EFT)还可以同时描述上述多种模型 (Frusciante & Perenon, n.d.)。 附录 6 中介绍了若干暗能量及修改引力模型。 现代宇宙学的一个重要课题就是通过宇宙学观测区分上述众多的不同模型,从而正确理解宇宙的演化。