4 结构增长
物质的原初扰动在引力作用下,经历线性增长及非线性增长两个阶段,逐渐形成今天我们看到的大尺度结构。 在线性阶段,我们可以借助扰动理论计算结构增长。 当演化进入非线性阶段,扰动理论不再适用,需要借助其他方法如N体数值模拟对结构增长进行计算。
4.1 扰动理论
为简化方程的表达,下面我们在共动坐标系下讨论问题。 定义共形时间\(\tau\)满足\(\rm{d} t=a(\tau)\rm{d} \tau\), 共形哈勃参数\(\mathscr{H}\equiv aH\),并用\({\bf x}\)以及\({\bf v}\)分别表示粒子的共动坐标,及共动坐标系下的本动速度。 则相空间中的物质分布函数\(f({\bf x}, {\bf p}, \tau )\)满足如下Vlasov方程: \[\begin{align} \frac{\rm{d} f}{\rm{d} \tau}=\frac{\partial f}{\partial \tau} + \frac{{\bf p}}{ma}\cdot \nabla f - ma \nabla \phi \cdot \frac{\partial f}{\partial {\bf p}}=0\ . \tag{4.1} \end{align}\] 其中,\(m\)为粒子质量,\(a\)为尺度因子,\({\bf p}=am{\bf v}\)为粒子动量。 \(\phi\)为引力势,满足泊松方程: \[\nabla^2\phi({\bf x}, \tau)=\frac{3}{2}\Omega_{\rm m}(\tau) \mathscr{H}^2(\tau )\delta({\bf x}, \tau)\ . \tag{4.2}\] \(\delta\)为密度涨落, \[\delta({{\bf x}, \tau}) \equiv \frac{\rho({{\bf x}, \tau})-\bar{\rho}}{\bar{\rho}}\ ,\] 其取值范围为\(-1<\delta<\infty\)。
4.1.1 欧拉扰动理论
直接求解Vlasov方程非常困难,我们通常更关心粒子空间分布的演化。 在欧拉坐标系下,相空间中的物质分布函数对动量求积分(即0阶矩),可以得到物质密度分布: \[\int \rm{d}^3{\bf p}f({\bf x}, {\bf p}, \tau)\equiv \rho({\bf x}, \tau)\ . \label{eqn:euler_delta}\] 其1阶矩与2阶矩分别为 \[\begin{align} &\int \rm{d}^3 {\bf p}\frac{{\bf p}}{am} f({\bf x}, {\bf p}, \tau) \equiv \rho({\bf x}, \tau){\bf v}({\bf x}, \tau)\ ,\\ &\int \rm{d}^3 {\bf p}\frac{p_ip_j}{(am)^2} f({\bf x}, {\bf p}, \tau) \equiv \rho({\bf x}, \tau){\bf v}_i({\bf x}, \tau){\bf v}_j({\bf x}, \tau)+\sigma_{ij}({\bf x}, \tau)\ . \end{align}\] 由物质守恒可得连续性方程: \[\begin{align} \frac{\partial \delta({\bf x}, \tau)}{\partial \tau} +\nabla \cdot \left[ 1+ \delta({\bf x}, \tau){\bf v}({\bf x}, \tau)\right]=0\ . \tag{4.3} \end{align}\] Vlasov方程(4.1)与连续性方程(4.3)联立可以给出描述动量守恒的欧拉方程: \[\frac{\partial {\bf v}({\bf x}, \tau)}{\partial \tau} + \mathscr{H}(\tau) {\bf v}({\bf x}, \tau)+{\bf v}({\bf x}, \tau)\cdot\nabla {\bf v}({\bf x}, \tau)= -\nabla\phi({\bf x}, \tau)-\frac{1}{\rho}\nabla_j(\rho\sigma_{ij})\ . \tag{4.4}\] 通过求解(4.3)与(4.4)可以得到密度场与速度场的演化方程。在线性近似下 \[\begin{align} &\frac{\partial \delta({\bf x}, \tau)}{\partial \tau}+\theta({\bf x}, \tau)=0\ ,\\ &\frac{\partial {\bf v}({\bf x}, \tau)}{\partial\tau}+\mathscr{H}(\tau) {\bf v}({\bf x}, \tau)=-\nabla \phi({\bf x}, \tau)\ . \end{align}\] 其中,\(\theta({\bf x}, \tau)\equiv \nabla\cdot {\bf v}({\bf x}, \tau)\)为速度场的散度。 令\(\delta({\bf x}, \tau)=D(\tau)\delta({\bf x}, 0)\),其中,\(D(\tau)\)为线性增长因子。 则\(\theta({\bf x}, \tau)=-\mathscr{H} f \delta({\bf x})\),其中,\(f\equiv \rm{d} \ln D/\rm{d} \ln a\)为线性增长率,描述结构增长的快慢。 对于一个由\(\Omega_{\rm m}\)与\(\Omega_{\Lambda}\)主导的宇宙, 可以解得,\(f\approx \Omega_{\rm m}^{0.55}(z)\)。 密度场满足方程: [^8] \[\ddot{\delta}+\left(\frac{3}{a}+\frac{\dot{H}}{H}\right)\dot{\delta}- \left( \frac{3}{2}\frac{\Omega_0 H_0^2}{H^2 a^3}\right) \left(\frac{\delta}{a^2}\right)=0\ .\]
4.1.2 拉格朗日扰动理论
欧拉方法可以通过微扰逐阶求解非线性扰动。在拉格朗日坐标下,也可以近似求解非线性扰动。 假设粒子初始位置为\({\bf q}\),在经历时间\(\tau\)后,其最终位置\({\bf x}\)可以由位移场\(\mathbf{\Psi}\)表示为 \[{\bf x}(\tau)={\bf q}+\mathbf{\Psi}({\bf q},\tau)\ .\] 位移场的运动方程为 \[\frac{\rm{d}^2{\bf x}}{\rm{d}\tau^2}+\mathscr{H}(\tau)\frac{\rm{d} {\bf x}}{\rm{d} \tau}=-\nabla \phi\ , \tag{4.5}\] \(\phi\)为引力势,满足泊松方程(4.2)。 对上式取散度可得 \[J({\bf q}, \tau)\nabla\cdot \left[\frac{\rm{d}^2\mathbf{\Psi}}{\rm{d} \tau^2}+\mathscr{H}(\tau)\frac{\rm{d}\mathbf{\Psi}}{\rm{d} \tau}\right] =\frac{3}{2}\Omega_{\rm m}\mathscr{H}^2(J-1)\ .\] 欧拉空间与拉格朗日空间质量守恒,有\(\bar{\rho}(1+\delta({\bf x}))\rm{d}^3x=\bar{\rho}\rm{d}^3q\)。 因此 \[1+\delta({\bf x})=\frac{1}{|\delta_{ij}+\Psi_{i, j}|}\equiv \frac{1}{J({\bf q}, \tau)}\ ,\] 其中,\(\Psi_{i, j}\equiv \partial \Psi_i/\partial {\bf q}_j\),\(J\)为欧拉空间转换到拉格朗日空间的雅可比矩阵。 位移场可以展开为\(\mathbf{\Psi}=\mathbf{\Psi}^{(1)}+\mathbf{\Psi}^{(2)}+\mathbf{\Psi}^{(3)}+\cdots\)。 运动方程(4.5)在一阶线性近似时的解满足: \[\nabla_q\cdot \mathbf{\Psi}^{(1)} = -D(\tau)\delta({\bf q})\ .\] 其中,\(D\)为线性结构增长因子。 此时 \[1+\delta({\bf x}, \tau)=\frac{1}{[1-\lambda_1D(\tau)][1-\lambda_2D(\tau)][1-\lambda_3D(\tau)]}\ .\] 其中,\(\lambda_i, \ i=1, 2, 3\)为\(\Psi_{i, j}\)的本征值。 该近似也被称为Zeldovich近似(ZA)。
4.2 N体数值模拟与非线性结构形成
4.2.1 N体数值模拟简介
如前所述,当演化进入非线性尺度后,传统的扰动理论以及解析模型已经无法精确描述此时的结构,需要借助数值模拟对结构演化进行计算。 通常数值模拟可以分为两大类:N体数值模拟与流体动力学(Hydrodynamical)数值模拟。 这些模拟在一定体积的三维盒子内模拟结构的形成及演化。 流体动力学模拟在星系形成及演化中应用更加广泛,通常有两种类型,一是基于平滑粒子(Smoothed-Particle Hydrodynamics, SPH), 一是基于格点(Grid-based)。 这里主要介绍与宇宙大尺度结构增长更相关的N体数值模拟。 N体数值模拟将物质视为离散分布的无碰撞粒子,每个粒子都携带一定质量,并且具有一定半径,在该半径内质量服从某种平滑分布。 模拟过程大致分为以下几步:
4.2.1.0.1 1. 设定初始条件。
初始条件一般设定在高红移处。 生成初始条件的方法有很多, 通常利用给定的根据功率谱,根据ZA或2阶拉格朗日扰动理论(2LPT)产生对应红移处的位移场, 进而生成初始的密度场及速度场。
4.2.1.0.2 2. 计算粒子受力。
粒子之间只存在引力,引力为长程力,因此在N体系统中,每两个粒子之间都需要计算一次相互作用。 对第\(i\)个粒子, \[{\bf F}_i=-\sum_{j\neq i} G \frac{{\bf r}_i-{\bf r}_j}{|{\bf r}_i-{\bf r}_j|^3}\ ,\] 这里假定了粒子具有单位质量。 \(\sum_{j\neq i}\)需要对所有\(j\neq i\)的粒子进行求和。 这种计算方法称为PP(Particle-Particle)算法。 PP算法的复杂度为\(\mathscr{O}(N^2)\),实际运用非常耗时,因此数值上衍生出了多种更快求解作用力的方法。
树算法(Tree)。 提出了八叉树算法。首先将盒子8等分,若子格子中的粒子数目多于1个,那么将子格子继续8等分, 以此类推,直至每个格子中最多只包含1个粒子。 从最大格点到最小格点,特征长度依次减半。 在计算受力时,从最大格点开始遍历,通过格子的大小及与粒子的距离来控制计算精度。 设格子的特征长度为\(\ell\),格子相对某一粒子的距离为\(d\), 若格子对该粒子的张角\(\theta=\ell/d\)小于设定的阈值, 则将该格子内所有粒子视为一个大质量粒子进行一次计算,否则进入下一层格子。 树算法的计算复杂度为\(\mathscr{O}(N\log N)\),缺点是需要消耗大量内存。
PM(Particle-Mesh)算法。 PM算法将盒子均分为若干个网格,将粒子对格点距离作为权重为邻近格点赋值,得到一个平滑分布的密度场\(\rho({\bf x})\)。 然后计算每个格点的受力 \({\bf F}_i=-\nabla \phi_i\),其中,\(\phi_i\)为第\(i\)个格点所在位置的引力势, 可通过求解泊松方程确定\(\nabla^2\phi=4\pi G\rho({\bf x})\)。 在傅立叶空间中,泊松方程变为 \(-k^2\phi({\bf k})=4\pi G \rho({\bf k})\),格点受力\({\bf F}_i=-i\phi({\bf k}){\bf k}\)。 如果盒子的大小远远大于感兴趣的尺度,那么\(\rho({\bf k})\)可以通过快速傅立叶变换(FFT)计算,显著提高计算速度。 最后,将格点受力用差值方法返还到粒子上。 PM算法的复杂度接近\(\mathscr{O}(N)\),但是格点数目会严重限制计算精度,想提高精度需要消耗大量内存及CPU。
混合算法。 为了在保证精度的同时提高计算速度,人们通常会混合使用上述的各种算法,如P\(^3\)M(Particle-Particle-Particle-Mesh)。 P\(^3\)M算法结合了PP算法与PM算法,在计算较近粒子间的受力时,采取PP算法;而在计算较远粒子间受力时,采取PM算法。 P\(^3\)M算法是运用最广泛的方法之一, 如下文中将要介绍的CosmicGrowth数值模拟。 除P\(^3\)M外,还有结合树算法与PM算法的tree-PM算法,如Gadget-2。
4.2.1.0.3 3. 更新每个粒子的位置及速度信息。
得到每个粒子受力后,需要计算下一时刻粒子的位置与速度。 为了保证计算收敛,满足能量守恒等条件,通常需要用到精确到二阶的时间积分器(integrator),如Leapfrog,速度和位置信息交替更新,每次移动半个时间步长。
4.2.1.0.5 CosmicGrowth系列数值模拟
表4.1与4.2列出了本文中用到的CosmicGrowth系列数值模拟的基本参数。 CosmicGrowth运行的为P\(^3\)M代码。 本文选取了其中两组不同参数的标准宇宙学模拟,Planck及WMAP。
| Model | \(\Omega_b\) $ | _c$ $ | mega_{}$ \(h\) | \(n_s\) | $ | _8$ |
|---|---|---|---|---|---|---|
| Planck \(\Lambda\)CDM | 0.0487 | 0.2663 | 0.685 0 | .673 0 | .9603 | 0.829 |
| WMAP \(\Lambda\)CDM | 0.0445 | 0.2235 | 0.732 0 | .71 0 | .968 | 0.83 |
| Name | \(N_\text{p}\) | \(L\) | \(\rm{d} a\) | \(\eta\) | \(z_i\) | \(N_\text{step}\) | \(z_{\text{out, 1}}\) | \(N_{\text{snap}}\) | Realizations | |
|---|---|---|---|---|---|---|---|---|---|---|
| Planck_2048_400 | \(2048^3\) | 400 | 0.0288 | 0.007 | 144 | 5000 | 16.87 | 100 | 1 | |
| Planck_2048_1200 | \(2048^3\) | 1200 | 0.06 | 0.03 | 72 | 1200 | 7.30 | 24 | 1 | |
| WMAP_2048_400 | \(2048^3\) | 400 | 0.0288 | 0.007 | 144 | 5000 | 16.87 | 100 | 1 | |
| WMAP_2048_1200 | \(2048^3\) | 1200 | 0.06 | 0.03 | 72 | 1200 | 7.30 | 24 | 1 | |
| WMAP_3072_600 | \(3072^3\) | 600 | 0.0288 | 0.01 | 144 | 5000 | 16.87 | 100 | 3 | |
| WMAP_3072_1200 | \(3072^3\) | 1200 | 0.0288 | 0.02 | 144 | 5000 | 16.87 | 100 | 1 |
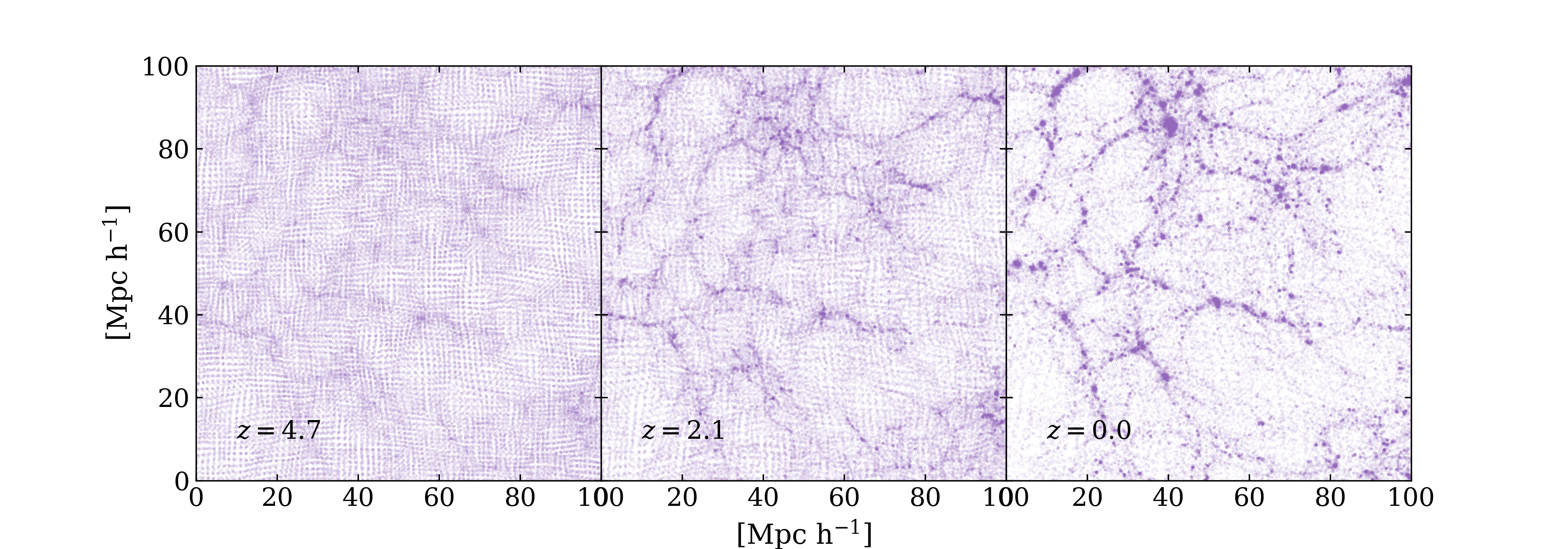
Figure 4.1: Modified Graivity Theories.
图4.1展示了CosmicGrowth中一个数值模拟在不同红移时的切片。 厚度为\(20\rm{Mpc}/h\)。在低红移处的宇宙物质结构形似神经网络,我们称之为宇宙网(Cosmic Web)。 宇宙网中的低密度区域为Void; 高密度区域主要由丝状结构的filament、以及filament交汇处的结点(knots)组成。 在这些高密度区域中会形成暗晕(halo)、子暗晕等高度非线性结构。
4.2.2 暗晕
暗晕是结构演化进入非线性阶段后形成的一类维里化结构。 描述暗晕形成最简单的理论是球塌缩模型。 在Einstein-de Sitter宇宙(\(\Omega_{\Lambda}=0\))中, 球塌缩模型给出的暗晕密度为\(\Delta_{\rm vir}= 18\pi^2\approx 178\)倍的背景密度。 如果半径\(R\)内的球形区域在红移\(z\)时开始塌缩,则线性理论给出\(z\)时区域内的平均密度为 \[\delta_c(z)=\frac{3(1+z)}{5}\left(\frac{3\pi}{2}\right)^{2/3}\ .\] 红移\(z=0\)时,\(\delta_c(z=0)\approx 1.686\)。 一个直接反映结构增长的统计量为暗晕的质量函数,其有多种表述形式, 常使用\(\rm{d} n/\rm{d} M\)或\(\rm{d} n/\rm{d} \ln M\), 其中,\(M\)表示暗晕质量,\(n\)表示暗晕个数。 显然,暗晕质量函数依赖红移与宇宙学。 总的来说,暗晕质量函数可以表示为 \[\frac{\rm{d} n}{\rm{d} M} = f(\sigma)\frac{\rho_{\rm m}}{M}\frac{\rm{d} \ln \sigma^{-1}}{\rm{d} M}\ ,\] 其中,\(\sigma\)为包含质量\(M\)的球体内的方均根扰动,\(f(\sigma)\)称为暗晕乘函数。 根据线性理论及球塌缩模型推导出了暗晕的质量分布函数,给出的乘函数的形式为 \[f(\sigma)=\sqrt{\frac{2}{\pi}}\frac{\delta_c}{\sigma}\exp\left(-\frac{\delta_c^2}{2\sigma^2}\right)\ .\] 但是,数值模拟显示,\(\delta_c\)与暗晕质量函数的实际值要明显大于上述理论的预言。 随后,等众多工作借助数值模拟, 在不同宇宙学下,给出了不同乘函数的拟合结果,具体形式可参考。